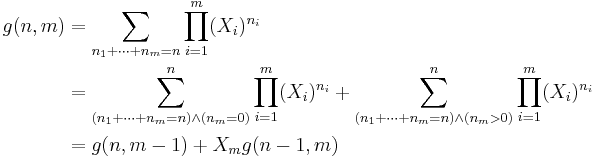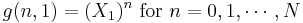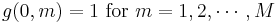Buzen's algorithm
In queueing theory, a discipline within the mathematical theory of probability, Buzen's algorithm is an algorithm for calculating the normalization constant G(K) in the Gordon–Newell theorem. This method was first proposed by Jeffrey P. Buzen in 1973.[1] Once G is computed the probability distributions for the network can be found. In contrast, mean value analysis is an alternative algorithm that can also be used to derive some performance measures (such as the mean queue lengths) without having to directly compute the normalization constant.
The motivation for this algorithm is efficiency: a straightforward Gordon-Newell calculation would require the enumeration of all states that the system can be in, resulting in a combinatorial explosion. Buzen's algorithm is of order N2, making the application of the G-N theorem practical, and opening up a large class of queueing systems to accurate modeling.
In the queuing literature Buzen's algorithm is sometimes also referred to as the convolution algorithm.
Contents |
Problem setup
Consider a closed queueing network with M service facilities and N circulating customers. Let 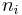 represent the number of customers present at the ith facility, with
represent the number of customers present at the ith facility, with 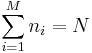 . We assume that the service time for a customer at the ith facility is given by an exponentially distributed random variable with mean
. We assume that the service time for a customer at the ith facility is given by an exponentially distributed random variable with mean 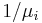 and that after completing service at the ith facility a customer will proceed to the jth facility with probability pij.
and that after completing service at the ith facility a customer will proceed to the jth facility with probability pij.
It follows from the Gordon–Newell theorem that the equilibrium distribution of customers in the network is given by:
where the 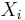 are found from the equations:
are found from the equations:
and G(N) is a normalizing constant such that the above probabilities sum to 1. [1]
The purpose of the Buzen algorithm is to numerically compute values of G.
Marginal distributions, expected number of customers
The general G-N distribution given above is mainly of theoretical interest. However, expressions for a number of useful performance measures can be derived from it. Buzen showed that the probability that there are exactly k customers at facility i is given by:
and the expected number of customers at facility i by
Note that these expressions also involve G. It is in the evaluation of these expressions that the algorithm is useful.
Derivation
The algorithm computes not just G but a two-dimensional function
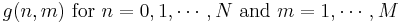 .
.
Once the calculation ends the values we are interested in are found by
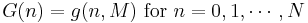 .
.
The definition of g and a recursive method of calculating it are as follows
Also
and
This recursive relationship allows for the calculation of all G(N) up to any value of N in order O(MN) time.
Implementation
It will be assumed that the Xm have been computed by solving the relevant equations and are available as an input to our routine. Although g is in principle a two dimensional matrix, it can be computed in a column by column fashion starting from the leftmost column. The routine uses a single column vector C to represent the current column of g.
C[0] := 1 for n := 1 step 1 until N do C[n] := 0; for m := 1 step 1 until M do for n := 1 step 1 until N do C[n] := C[n] + X[m]*C[n-1];
At completion, C contains the desired values G(0), G(1) to G(N). [1]
References
- ^ a b c Buzen, Jeffrey (September 1973). "Computational algorithms for closed queueing networks with exponential servers". Communications of the ACM 16 (9): 527. doi:10.1145/362342.362345. [1]
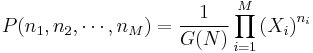
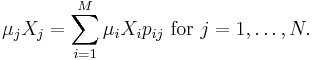
![P(n_i = k) = \frac{X_i^k}{G(N)}[G(N-k) - X_i G(N-k-1)]](/2012-wikipedia_en_all_nopic_01_2012/I/87170312ba493b1074a35a5c6bbe7f62.png)
![E[n_i] = \sum_{k=1}^N X_i^k \frac{G(N-k)}{G(N)}.](/2012-wikipedia_en_all_nopic_01_2012/I/05e82f232960804fae463bd3d58027a2.png)